Hi,
I have been browsing the old posts trying to understand the theory behind the IB type metal detector. What I am most interested in is to estimate the level of the RX signal. I know that there are a lot of factors in this, and maybe it would be easier to make a measurement, but if someone knows the equations or a paper I'd be grateful.
For example if one were to build a sinewave 10KHz TX with 8 inch 5 mH coil with a 10V p-p swing. And use a similar coil for the RX what would be the RX level in milli or microvolts of a penny in air 8 inches below the coil? What about in typical ground at 3 inches?
Thanks,
Harry
I have been browsing the old posts trying to understand the theory behind the IB type metal detector. What I am most interested in is to estimate the level of the RX signal. I know that there are a lot of factors in this, and maybe it would be easier to make a measurement, but if someone knows the equations or a paper I'd be grateful.
For example if one were to build a sinewave 10KHz TX with 8 inch 5 mH coil with a 10V p-p swing. And use a similar coil for the RX what would be the RX level in milli or microvolts of a penny in air 8 inches below the coil? What about in typical ground at 3 inches?
Thanks,
Harry

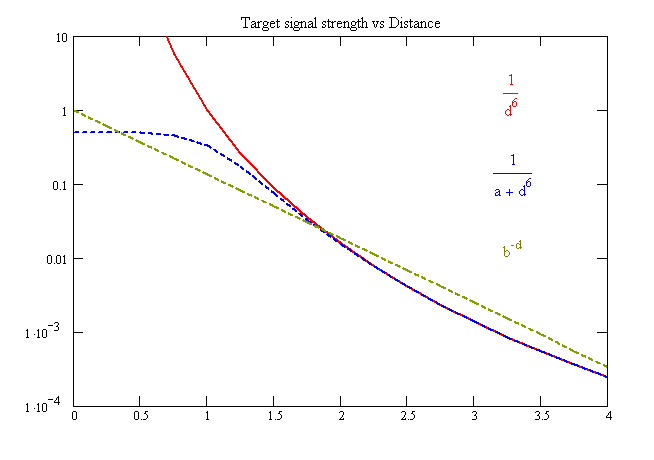
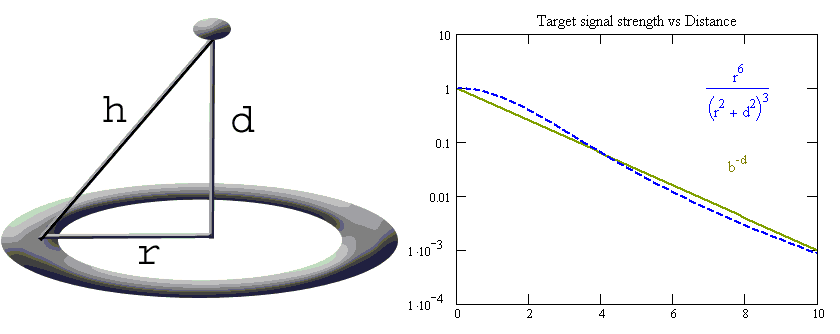
Comment