PI limit to early sampling

[green]

Tried a square wave input, easier to see response. (_2) 10 and 50usec sample time with R5(R22 MPP) 56k, (_3) 10 and 50usec sample time with R5(R22 MPP) 150k. Not what I was expecting, maybe something wrong with my simulation.

There is something wrong with the simulation. EF sample time sample time 10usec instead of 50usec causes the overshoot. Looks good when both sample times 50usec. (target sample time=EF sample time)

[green]

I contacted Eric, and he will provide the circuits when he has some spare time.

In your post you stated that you wanted to run an AC analysis on the MPP integrator. However, your waveforms are from a time domain analysis.
Have a look at the analysis command in the schematic. It says ".time" in both cases instead of ".ac".
An AC analysis is also known as a small-signal AC analysis. The simulator linearises the models around the current operating point, and therefore the results are only good for small signal changes. For a large-signal analysis you would need to use a different technique known as harmonic balance simulation, but this is not available in LTSpice. Also, even if you set up the analysis as AC, the switches (or even fets used as switches) are essentially time domain devices, so the results of an AC analysis would be nonsensical.

Your only option is to run the simulation in the time domain, and then perform an FFT on the results. However, I'm sure just how useful the results will be in that case.

I was thinking AC analysis for a easy way to determine cutoff frequency when changing %sample time or changing R22(MPP). What would be a good way to determine cutoff frequency?

If the switches are time domain. Is there away to replace the integrator input signal with a noise source(resistor noise times some gain) and look at integrator out noise signal in the time domain to see the effect of changing sample times or sample rate on noise?

[moodz]

Thanks for the reply. When I replied (Eric hasn't posted any circuits), it was about using spice for modeling circuits reply #76. I tried the MPP integrator because I've never understood how it works.

Not sure how the MPP integrator delivers faster sampling time. #76 is about simulating a 10x faster tx rate with 1/10 current. #3 cct in the thread i mentioned above can do it. I have simulated and built it with tx rates up to 100 khz.

[green]

Not sure how the MPP integrator delivers faster sampling time. #76 is about simulating a 10x faster tx rate with 1/10 current. #3 cct in the thread i mentioned above can do it. I have simulated and built it with tx rates up to 100 khz.

[How do the two configurations compare for early sampling, noise reduction and target signal at integrator output?

Anyone prepared to give it a go?] from reply #76



How do we compare noise reduction at integrator output with LT spice?

[Ferric Toes]

I think you will find he has published some ccts here .... http://www.geotech1.com/forums/showt...640#post223640

Particularly post number #3 ... its so close to a a very significant improvement in PI performance .. its one step away


You may also refer to the PUBLISHED PRIOR ART ...

Sample and hold demodulator with feedback for reduced riffle
US 4617521 A

I was retired and had time to work on this ... I lodged a provisional patent ... however now that I am back in the workforce and no time so I am putting it out there ...

Eric's circuits are briliant ... a few tweaks and they will shine even more. RE: ferrite discrimination ;-)

moodz

Hi Moodz,

You got me thinking about these old circuits. Yes, I think I can see how a few tweeks might help with the ferrite problem. Also the wet sand problem on a beach? .

Eric.

[moodz]

[How do the two configurations compare for early sampling, noise reduction and target signal at integrator output?

Anyone prepared to give it a go?] from reply #76



How do we compare noise reduction at integrator output with LT spice?

Are you able to clarify what noise you are trying to reduce ? ... my biggest problems in real circuits have been mains induced hum, Earth field, hot rocks ( magnetic ) and power supply noise ... some of these can be approximated in ltspice. Low frequency noise contributed from the integrator opamp itself will occur at high gains. Unfortunately the spec sheets are of no help here as manufacturers specify optimum noise figures for their devices not at low frequency. Another example is power supply noise ... even with a synchronised power supply there is self demodulation component added as a low frequency variance in the demod ouput that requires dithering or similiar to counteract.

[green]

Are you able to clarify what noise you are trying to reduce ? ... my biggest problems in real circuits have been mains induced hum, Earth field, hot rocks ( magnetic ) and power supply noise ... some of these can be approximated in ltspice. Low frequency noise contributed from the integrator opamp itself will occur at high gains. Unfortunately the spec sheets are of no help here as manufacturers specify optimum noise figures for their devices not at low frequency. Another example is power supply noise ... even with a synchronised power supply there is self demodulation component added as a low frequency variance in the demod ouput that requires dithering or similiar to counteract.

I was hoping I could look at integrator out with a random input(resistor, amplifier noise) to see if it looked similar to what I see on the bench circuit with a scope. Tried the spice integrator(sample rate=1000Hz, target sample=10usec, EF sample=10usec) integrator input=.1 volt sine wave at 5Hz, 1005Hz, 50005Hz. Integrator out was the same 5Hz signal at the same amplitude for the three inputs, matches sampling theory. I can't find what sampling theory predicts for a random input with no antialiasing filter to verify the bench circuit makes sense.

[eclipse]

You may want to check out the suggestion for LPF filter after the integrator, and perhaps a little change - C1 to 330nF/470nF to increase fc.

[moodz]

I was hoping I could look at integrator out with a random input(resistor, amplifier noise) to see if it looked similar to what I see on the bench circuit with a scope. Tried the spice integrator(sample rate=1000Hz, target sample=10usec, EF sample=10usec) integrator input=.1 volt sine wave at 5Hz, 1005Hz, 50005Hz. Integrator out was the same 5Hz signal at the same amplitude for the three inputs, matches sampling theory. I can't find what sampling theory predicts for a random input with no antialiasing filter to verify the bench circuit makes sense.

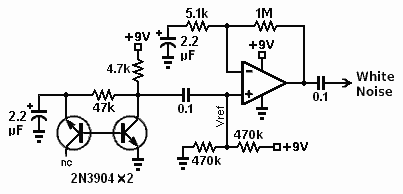
This link is a good example of how to use ltspice for noise analysis. Noise sources can be random or white or adapted to suit your requirements.

http://www.simonbramble.co.uk/techar..._amp_noise.htm

[Qiaozhi]

I was hoping I could look at integrator out with a random input(resistor, amplifier noise) to see if it looked similar to what I see on the bench circuit with a scope. Tried the spice integrator(sample rate=1000Hz, target sample=10usec, EF sample=10usec) integrator input=.1 volt sine wave at 5Hz, 1005Hz, 50005Hz. Integrator out was the same 5Hz signal at the same amplitude for the three inputs, matches sampling theory. I can't find what sampling theory predicts for a random input with no antialiasing filter to verify the bench circuit makes sense.

This might be what you're actually looking for ->
http://electronics.stackexchange.com...e-with-ltspice

[green]

This might be what you're actually looking for ->
http://electronics.stackexchange.com...e-with-ltspice

Thanks, looks like just what I was looking for.

[green]

Thanks, looks like just what I was looking for.

Seems to be doing what I want. Couple questions. How to calculate the cutoff frequency of the MPP integrator? What does the statement in the LT spice noise generator mean, V= (white (2e6*time) / 10)?

[Qiaozhi]

What does the statement in the LT spice noise generator mean, V= (white (2e6*time) / 10)?

The equation for the white noise source is V = white(x * time) * Y
The current time of the simulator is used as a seed for the random number generator, which creates an output between -0.5V and +0.5V.
You can use the Y parameter to scale this output. So, in your example Y = 0.1, and the output will swing between -50mV and +50mV.
The X parameter affects the spectrum of the noise. Try different X values to see how the output changes.

By the way, the random noise source generates a consistent (repeatable) set of random numbers (if that makes sense). If it was truly random, you would never be able to reproduce the same set of results each time you ran the simulation. To get a different set of random numbers you have to change the seed.

[ivconic]

[green]

LT spice, 1C integrator white noise example. Top example gain=10, middle and bottom example gain=100. Middle and bottom, noise increased about 2.5 times giving an increase in S/N of about 4 times.